Lecture 4: The Cross Product
Alright class, welcome back. In our last lecture, we explored the dot product, which takes two vectors and gives us a scalar that tells us how much they point in the same direction. Today, we'll learn about our second type of vector multiplication: the cross product. This operation is completely different. It takes two vectors and gives back a new vector—one with a very special geometric property: it's perpendicular to both of the original vectors.
Why would we want to do this? Imagine you have a flat tabletop defined by two vectors lying on its surface. How would you find a vector that points straight up, perfectly perpendicular to the table? The cross product is the tool for the job. This has huge applications in physics for things like torque, angular momentum, and magnetic fields, and in computer graphics for calculating lighting.
Topic 1: How Do We Find a Perpendicular Vector?
Before I show you the standard formula, let's think about how we could build a vector that we know is orthogonal to two others. Let's say we have our two vectors, $\mathbf{a} = \langle a_1, a_2, a_3 \rangle$ and $\mathbf{b} = \langle b_1, b_2, b_3 \rangle$. We are looking for a new vector, $\mathbf{x} = \langle x, y, z \rangle$, that is perpendicular to both of them.
Our test for perpendicularity is the dot product! So, we need to find an $\mathbf{x}$ that satisfies two conditions:
- $\mathbf{a} \cdot \mathbf{x} = a_1x + a_2y + a_3z = 0$
- $\mathbf{b} \cdot \mathbf{x} = b_1x + b_2y + b_3z = 0$
Solving this system of two equations with three unknowns leads to the solution that forms the components of the cross product. The determinant formula is a clever mnemonic for this algebraic solution.
💡 The Insight
The standard determinant formula for the cross product is not some magical incantation. It is simply a mnemonic—a brilliant memory aid for performing the exact algebraic steps required to find a vector that satisfies the two orthogonality conditions above. We're using it because it's a reliable way to get the right answer, but the foundation comes from solving that system of equations.
Topic 2: The Algebraic Definition of the Cross Product
With that insight in mind, let's look at the computational tool everyone uses. The cross product is calculated using the determinant of a special 3x3 matrix.
Definition of the Cross Product (Determinant Form)
If $\mathbf{a} = \langle a_1, a_2, a_3 \rangle$ and $\mathbf{b} = \langle b_1, b_2, b_3 \rangle$, their cross product is:
$$ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $$We expand this along the first row:
$$ \mathbf{a} \times \mathbf{b} = \mathbf{i} \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix} - \mathbf{j} \begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix} + \mathbf{k} \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} $$ $$ = (a_2b_3 - a_3b_2)\mathbf{i} - (a_1b_3 - a_3b_1)\mathbf{j} + (a_1b_2 - a_2b_1)\mathbf{k} $$Watch out for that minus sign on the $\mathbf{j}$ component! It's the most common place to make a mistake.
Example: Calculating a Cross Product
Let's find the cross product of $\mathbf{a} = \langle 2, 1, -1 \rangle$ and $\mathbf{b} = \langle -3, 4, 1 \rangle$.
$$ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & 1 & -1 \\ -3 & 4 & 1 \end{vmatrix} $$
$$ = \mathbf{i}((1)(1) - (-1)(4)) - \mathbf{j}((2)(1) - (-1)(-3)) + \mathbf{k}((2)(4) - (1)(-3)) $$
$$ = \mathbf{i}(1 - (-4)) - \mathbf{j}(2 - 3) + \mathbf{k}(8 - (-3)) $$
$$ = 5\mathbf{i} - (-1)\mathbf{j} + 11\mathbf{k} = \langle 5, 1, 11 \rangle $$
Verification: Let's check if this new vector is orthogonal to $\mathbf{a}$ and $\mathbf{b}$ by using the dot product.
$$ \langle 5, 1, 11 \rangle \cdot \langle 2, 1, -1 \rangle = (5)(2) + (1)(1) + (11)(-1) = 10 + 1 - 11 = 0 $$
$$ \langle 5, 1, 11 \rangle \cdot \langle -3, 4, 1 \rangle = (5)(-3) + (1)(4) + (11)(1) = -15 + 4 + 11 = 0 $$
It works! The resulting vector is indeed orthogonal to both original vectors.
Check Your Understanding:
Problem: Find the cross product of $\mathbf{u} = \langle 1, -2, 1 \rangle$ and $\mathbf{v} = \langle 3, 1, -2 \rangle$.
Topic 3: Geometric Meaning: Direction and Magnitude
Now that we know how to calculate it, let's understand what the cross product represents geometrically.
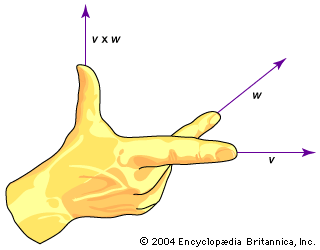
Direction: The Right-Hand Rule
The cross product is orthogonal to the two original vectors, and the Right-Hand Rule tells us which of the two possible perpendicular directions it points. To use the rule, point the fingers of your right hand in the direction of the first vector ($\mathbf{a}$). Curl your fingers toward the direction of the second vector ($\mathbf{b}$). Your thumb now points in the direction of $\mathbf{a} \times \mathbf{b}$.
Cross Product (v x w)
Torque from Force
Force from Magnetic Field
Magnitude: Area of a Parallelogram
The magnitude of the cross product vector has a beautiful geometric interpretation: it is the area of the parallelogram formed by the two vectors.
Magnitude of the Cross Product
If $\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$, then the magnitude is:
$$ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin(\theta) $$This is precisely the formula for the area of a parallelogram: Area = base × height = $|\mathbf{a}| \cdot (|\mathbf{b}|\sin(\theta))$.
Example: Finding the Area of a Parallelogram
Find the area of the parallelogram with adjacent sides given by $\mathbf{a} = \langle 2, 1, -1 \rangle$ and $\mathbf{b} = \langle -3, 4, 1 \rangle$.
From our previous example, we know that $\mathbf{a} \times \mathbf{b} = \langle 5, 1, 11 \rangle$. The area of the parallelogram is the magnitude of this vector.
$$ \text{Area} = |\mathbf{a} \times \mathbf{b}| = |\langle 5, 1, 11 \rangle| = \sqrt{5^2 + 1^2 + 11^2} = \sqrt{25 + 1 + 121} = \sqrt{147} $$
Check Your Understanding:
Problem: Find the area of the triangle with vertices P(1, 1, 1), Q(2, 3, 4), and R(4, 3, 2). (Hint: A triangle is half of a parallelogram!)
Topic 4: Properties of the Cross Product
The cross product has some algebraic properties that are similar to normal multiplication, but with one crucial, surprising difference.
Cross Product Properties
If $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ are vectors and c is a scalar:
- $\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})$ (Anti-commutative)
- $\mathbf{a} \times \mathbf{a} = \mathbf{0}$ (The cross product of parallel vectors is the zero vector)
- $(c\mathbf{a}) \times \mathbf{b} = c(\mathbf{a} \times \mathbf{b}) = \mathbf{a} \times (c\mathbf{b})$ (Scalar Associativity)
- $\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}$ (Distributive Property)
The most important property to remember is the first one. If you switch the order, you negate the vector! This makes sense from the Right-Hand Rule—reversing the order makes your thumb point the opposite way.
Check Your Understanding:
Problem: If you know that $\mathbf{u} \times \mathbf{v} = \langle 2, -3, 5 \rangle$, what is $\mathbf{v} \times \mathbf{u}$? What is $(2\mathbf{u}) \times \mathbf{v}$?
Topic 5: The Scalar Triple Product and Volume
What happens if we combine our two vector products? The Scalar Triple Product mixes a dot product with a cross product to tell us something about volume.
The Scalar Triple Product
The scalar triple product is written as $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$. Its absolute value represents the volume of the parallelepiped (a slanted box) formed by the three vectors.
It can be calculated with a single determinant:
$$ \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} $$If the scalar triple product is 0, it means the volume is 0, so the three vectors must lie on the same plane. We call them coplanar.
Example: Calculating Volume
Find the volume of the parallelepiped determined by vectors $\mathbf{a} = \langle 1, 2, 3 \rangle$, $\mathbf{b} = \langle -1, 1, 2 \rangle$, and $\mathbf{c} = \langle 2, 1, 4 \rangle$.
$$ V = \left| \begin{vmatrix} 1 & 2 & 3 \\ -1 & 1 & 2 \\ 2 & 1 & 4 \end{vmatrix} \right| $$
$$ V = |1((1)(4) - (2)(1)) - 2((-1)(4) - (2)(2)) + 3((-1)(1) - (1)(2))| $$
$$ V = |1(2) - 2(-8) + 3(-3)| = |2 + 16 - 9| = |9| = 9 $$
The volume is 9 cubic units.
Check Your Understanding:
Problem: Use the scalar triple product to determine if the vectors $\mathbf{u} = \langle 1, 4, -7 \rangle$, $\mathbf{v} = \langle 2, -1, 4 \rangle$, and $\mathbf{w} = \langle 0, -9, 18 \rangle$ are coplanar.
Topic 6: Application - Torque
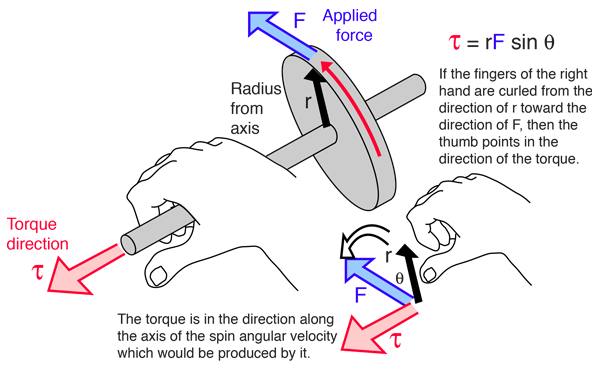
One of the most important physical applications of the cross product is in calculating torque.
Formula for Torque
In physics, torque $\mathbf{\tau}$ is a measure of the turning force on an object. It's a vector calculated as the cross product of the position vector $\mathbf{r}$ (from the pivot to the point of force) and the force vector $\mathbf{F}$.
$$ \mathbf{\tau} = \mathbf{r} \times \mathbf{F} $$Example: Torque on a Wrench
A force of $\mathbf{F} = \langle 0, -40, 0 \rangle$ N (40 N straight down) is applied to a wrench at the point $\mathbf{r} = \langle 0.2, 0.1, 0 \rangle$ m. Find the torque vector.
$$ \mathbf{\tau} = \mathbf{r} \times \mathbf{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0.2 & 0.1 & 0 \\ 0 & -40 & 0 \end{vmatrix} $$
$$ = \mathbf{i}((0.1)(0) - (0)(-40)) - \mathbf{j}((0.2)(0) - (0)(0)) + \mathbf{k}((0.2)(-40) - (0.1)(0)) $$
$$ = 0\mathbf{i} - 0\mathbf{j} - 8\mathbf{k} = \langle 0, 0, -8 \rangle $$
The torque is 8 N·m, and the negative $\mathbf{k}$ direction indicates it causes a clockwise rotation around the z-axis (tightening the bolt).
Bridging the Gap: Why is Torque a Cross Product?
It can seem strange that a formula related to "area" somehow measures rotational force. The key is to think of the magnitude $|\mathbf{r} \times \mathbf{F}| = |\mathbf{r}||\mathbf{F}|\sin(\theta)$ not as an area, but as the perfect recipe for leverage.
- Lever Arm ($|\mathbf{r}|$): This is the length of your wrench. A longer wrench gives more leverage.
- Force ($|\mathbf{F}|$): This is how hard you push on the wrench. More force means more leverage.
- Angle ($\sin(\theta)$): This is the crucial part. Pushing or pulling along the wrench ($\theta=0^\circ$) does nothing. Your force is most effective when it is perpendicular to the wrench ($\theta=90^\circ$). The $\sin(\theta)$ term perfectly captures this: it's 0 when the angle is 0, and maximum (1) when the angle is 90°.
So, the cross product's magnitude precisely models the physics of leverage. Furthermore, the direction of the resulting vector gives you the axis of rotation (e.g., pointing along the z-axis for a bolt on the xy-plane), telling you whether you're tightening or loosening it. It's a perfect marriage of math and physics.
Check Your Understanding:
Problem: A force of $\mathbf{F} = \langle 4, 5, 0 \rangle$ N is applied to a lever at a point with position vector $\mathbf{r} = \langle 1, 2, 0 \rangle$ m, relative to the pivot. Find the torque vector $\mathbf{\tau}$ and its magnitude.
Conclusion
The cross product is our tool for producing perpendicular vectors in 3D space. It's a completely different kind of multiplication from the dot product. The dot product gives a scalar and measures alignment, while the cross product gives a vector and measures perpendicularity and area. It's anti-commutative, its magnitude gives the area of a parallelogram, and when combined with the dot product, it reveals the volume of a parallelepiped.
In our next lecture, we're going to put this tool to immediate use as we derive the equations for lines and planes in space. You'll see that finding a normal vector with the cross product is the essential first step for defining any plane. See you then! 🚀