Lecture 3: The Dot Product
Alright class, welcome back. So far, we've learned how to add vectors and multiply them by scalars. Today, we're going to explore a way to multiply two vectors together. There are actually two important ways to do this, and we'll start with the first, called the dot product. To see why this operation is useful, let's begin with a practical example.
Topic 1: A Practical Motivation: Calculating Revenue
Example: The Street Vendor
A street vendor sells a hamburgers, b hot dogs, and c bottles of water on a given day. He charges \$4 for a hamburger, \$2.50 for a hot dog, and \$1 for water.
We can represent the quantity of items sold as a vector:
And the price of each item as a vector:
If we multiply the corresponding components of these two vectors and add the results, we get:
This expression represents the total daily revenue. This operation—multiplying corresponding components and summing them up—is exactly what the dot product does. It's a fundamental operation in computing and data science for calculating weighted sums, and it shows up everywhere.
Check Your Understanding:
Problem: A coffee shop sells s small, m medium, and l large coffees for \$2.50, \$3.50, and \$4.50 respectively. Create a quantity vector $\mathbf{Q}$ and a price vector $\mathbf{P}$, and explain what the dot product $\mathbf{Q} \cdot \mathbf{P}$ represents.
Topic 2: The Algebraic Definition and Properties
Now that we have a practical motivation, let's formally define the dot product and look at its properties.
Definition of the Dot Product (Component Form)
If $\mathbf{a} = \langle a_1, a_2, a_3 \rangle$ and $\mathbf{b} = \langle b_1, b_2, b_3 \rangle$, then the dot product of $\mathbf{a}$ and $\mathbf{b}$ is:
$$ \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3 $$Notice the result is a scalar (a single number), not another vector!
Properties of the Dot Product
The dot product follows several familiar algebraic rules. If a, b, and c are vectors and c is a scalar, then:
- Commutative Property: $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$
- Distributive Property: $\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}$
- Scalar Multiplication: $(c\mathbf{a}) \cdot \mathbf{b} = c(\mathbf{a} \cdot \mathbf{b}) = \mathbf{a} \cdot (c\mathbf{b})$
- Norm Squared: $\mathbf{a} \cdot \mathbf{a} = |\mathbf{a}|^2$
Example: Finding Magnitude with the Dot Product
Let's find the length of the vector $\mathbf{w} = \langle 3, 4, 1 \rangle$. We know from the last lecture that we can use the distance formula: $|\mathbf{w}| = \sqrt{3^2 + 4^2 + 1^2} = \sqrt{26}$.
Let's see how the dot product property gives us the same result. $$ \mathbf{w} \cdot \mathbf{w} = \langle 3, 4, 1 \rangle \cdot \langle 3, 4, 1 \rangle = (3)(3) + (4)(4) + (1)(1) = 9 + 16 + 1 = 26 $$ Since $\mathbf{w} \cdot \mathbf{w} = |\mathbf{w}|^2$, we have $|\mathbf{w}|^2 = 26$, which means $|\mathbf{w}| = \sqrt{26}$. It's the same thing!
Check Your Understanding:
Problem: Use the dot product to find the magnitude of the vector $\mathbf{v} = \langle 2, -1, 3 \rangle$.
Topic 3: The "Why" - A Little Bit of History and Geometric Insight
The dot product can feel a bit mysterious at first. Why define multiplication this way? It arose in the late 19th century as physicists and mathematicians were looking for a simpler way to handle calculations involving forces and angles. They wanted a tool that could easily answer a very common physical question: "How much of one vector's influence is acting in the direction of another vector?" This insight provides the bridge to its geometric meaning.
Topic 4: The Geometric Meaning of the Dot Product
Let's explore that physical intuition with a thought experiment. Imagine we have vector $\mathbf{a}$ and vector $\mathbf{b}$, with an angle $\theta$ between them. We can ask how much of one vector's influence (like a force) acts along the direction of the other (like a displacement). In physics, this concept is called work.
The component of force $\mathbf{b}$ that acts along the direction of $\mathbf{a}$ has a magnitude of $|\mathbf{b}|\cos(\theta)$. The work done is this component of force multiplied by the distance, which is $|\mathbf{a}|$. So, $W = (|\mathbf{b}|\cos\theta) |\mathbf{a}|$. Due to commutativity, this is the same as $(|\mathbf{a}|\cos\theta) |\mathbf{b}|$. This symmetric quantity is what we define as the dot product.
The Dot Product, Geometric Version
If $\theta$ is the angle between two non-zero vectors $\mathbf{a}$ and $\mathbf{b}$, then:
$$ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos(\theta) $$We can also rearrange this formula to solve for the angle:
$$ \cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|} $$Example: Finding the Angle Between Two Vectors
Let's find the angle between the vectors $\mathbf{a} = \langle 1, 2, -2 \rangle$ and $\mathbf{b} = \langle 3, 0, 4 \rangle$.
Step 1: Calculate the dot product.
$$ \mathbf{a} \cdot \mathbf{b} = (1)(3) + (2)(0) + (-2)(4) = 3 + 0 - 8 = -5 $$
Step 2: Calculate the magnitudes.
$$ |\mathbf{a}| = \sqrt{1^2 + 2^2 + (-2)^2} = \sqrt{1+4+4} = \sqrt{9} = 3 $$
$$ |\mathbf{b}| = \sqrt{3^2 + 0^2 + 4^2} = \sqrt{9+0+16} = \sqrt{25} = 5 $$
Step 3: Use the formula to find the angle.
$$ \cos(\theta) = \frac{-5}{(3)(5)} = \frac{-5}{15} = -\frac{1}{3} $$
$$ \theta = \arccos\left(-\frac{1}{3}\right) \approx 109.5^\circ $$
Check Your Understanding:
Problem: Find the angle $\theta$ between the vectors $\mathbf{u} = \langle 2, 1, -2 \rangle$ and $\mathbf{v} = \langle 0, 3, 4 \rangle$.
Topic 5: Orthogonal Vectors
The most important angle to check for is a right angle, $90^\circ$. We have a special name for this: orthogonal, which is just a fancier word for perpendicular. Since we know that $\cos(90^\circ) = 0$, the dot product gives us a dead simple test for orthogonality.
Test for Orthogonality
Two vectors $\mathbf{a}$ and $\mathbf{b}$ are orthogonal if and only if $\mathbf{a} \cdot \mathbf{b} = 0$.
Check Your Understanding:
Problem: Are the vectors $\mathbf{u} = \langle 2, 2, -1 \rangle$ and $\mathbf{v} = \langle 5, -4, 2 \rangle$ orthogonal?
Topic 6: Direction Angles and Direction Cosines
We can also use the dot product to find the angles that a single vector makes with the positive coordinate axes. These are called the direction angles, denoted $\alpha$, $\beta$, and $\gamma$ for the x, y, and z-axes, respectively. Their cosines are called the direction cosines.
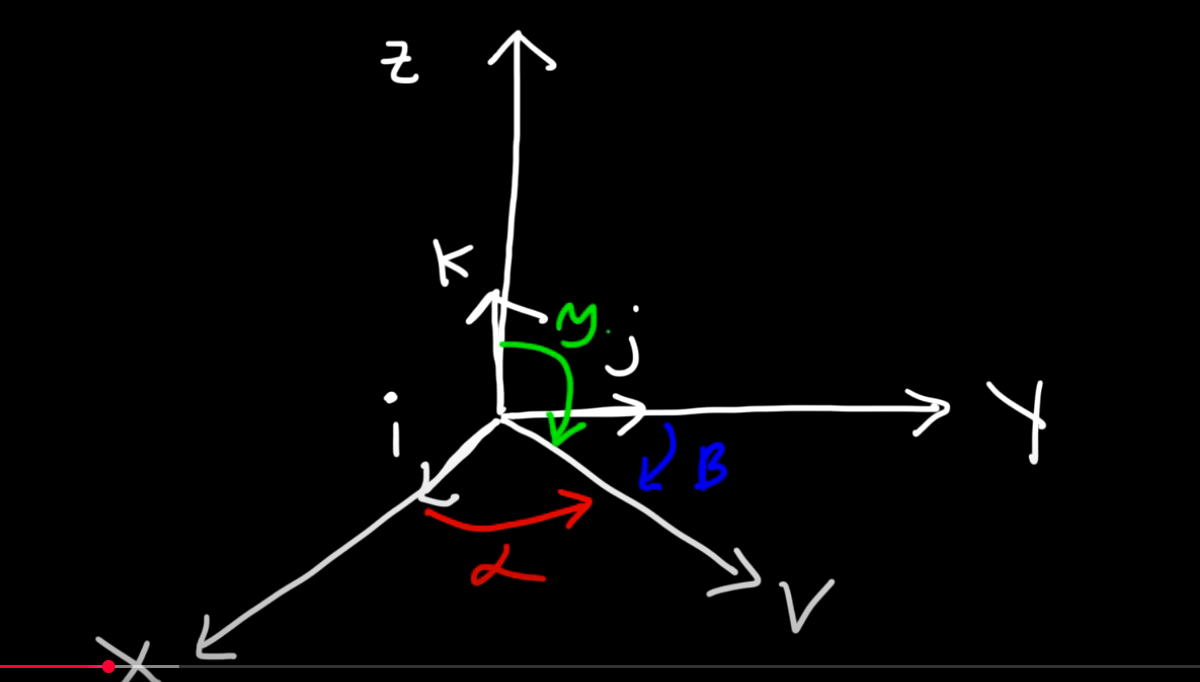
Direction Cosines
For a vector $\mathbf{a} = \langle a_1, a_2, a_3 \rangle$:
$$ \cos(\alpha) = \frac{a_1}{|\mathbf{a}|}, \quad \cos(\beta) = \frac{a_2}{|\mathbf{a}|}, \quad \cos(\gamma) = \frac{a_3}{|\mathbf{a}|} $$This comes from dotting $\mathbf{a}$ with the basis vectors $\mathbf{i}=\langle 1,0,0 \rangle$, $\mathbf{j}=\langle 0,1,0 \rangle$, and $\mathbf{k}=\langle 0,0,1 \rangle$.
Example: Finding Direction Cosines
Find the direction cosines of the vector $\mathbf{v} = \langle 1, 2, 3 \rangle$.
First, we find the magnitude: $|\mathbf{v}| = \sqrt{1^2+2^2+3^2} = \sqrt{1+4+9} = \sqrt{14}$.
Now we can find the direction cosines:
$$ \cos(\alpha) = \frac{1}{\sqrt{14}}, \quad \cos(\beta) = \frac{2}{\sqrt{14}}, \quad \cos(\gamma) = \frac{3}{\sqrt{14}} $$
Check Your Understanding:
Problem: Find the direction angles $\alpha, \beta,$ and $\gamma$ for the vector $\mathbf{a} = \langle 4, 0, -3 \rangle$.
Topic 7: Projections
Now we come back to that key physical idea: "How much of one vector acts in the direction of another?" The mathematical tool for this is called a projection. You can think of it as the "shadow" that one vector casts onto another. This is an incredibly important idea that we will use later to calculate the work done by a force and to find the closest distance from a point to a line.
Vector and Scalar Projections
The scalar projection of $\mathbf{b}$ onto $\mathbf{a}$ is the signed length of the shadow:
$$ \text{comp}_{\mathbf{a}} \mathbf{b} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|} $$The vector projection of $\mathbf{b}$ onto $\mathbf{a}$ is the actual shadow vector itself:
$$ \text{proj}_{\mathbf{a}} \mathbf{b} = \left(\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|^2}\right) \mathbf{a} $$This formula just takes the length (the scalar projection) and multiplies it by a unit vector in the direction of $\mathbf{a}$ to give it the correct direction.
Example: Finding Projections
Let's find the scalar and vector projections of $\mathbf{b} = \langle 1, 1, 2 \rangle$ onto $\mathbf{a} = \langle -2, 3, 1 \rangle$.
First, we need the dot product and the magnitude of $\mathbf{a}$:
$$ \mathbf{a} \cdot \mathbf{b} = (-2)(1) + (3)(1) + (1)(2) = -2 + 3 + 2 = 3 $$
$$ |\mathbf{a}| = \sqrt{(-2)^2 + 3^2 + 1^2} = \sqrt{4+9+1} = \sqrt{14} $$
Now we can find the scalar projection:
$$ \text{comp}_{\mathbf{a}} \mathbf{b} = \frac{3}{\sqrt{14}} $$
And the vector projection:
$$ \text{proj}_{\mathbf{a}} \mathbf{b} = \frac{3}{(\sqrt{14})^2} \langle -2, 3, 1 \rangle = \frac{3}{14} \langle -2, 3, 1 \rangle = \left\langle -\frac{3}{7}, \frac{9}{14}, \frac{3}{14} \right\rangle $$
Check Your Understanding:
Problem: Find the scalar and vector projections of $\mathbf{b} = \langle 1, 0, 2 \rangle$ onto $\mathbf{a} = \langle 2, -2, 1 \rangle$.
Topic 8: Application - Calculating Work
One of the classic applications of the dot product is in calculating Work. In physics, work is done only when a force causes a displacement. Furthermore, only the component of the force that is in the direction of the displacement counts.
Example: Work Done by a Force
A wagon is pulled a distance of 100m along a horizontal path by a constant force of 70 N. The handle of the wagon is held at an angle of 35° above the horizontal. Find the work done.
Let's represent the force and displacement as vectors. The displacement vector is $\mathbf{D} = \langle 100, 0 \rangle$. The force vector is $\mathbf{F} = \langle 70\cos(35^\circ), 70\sin(35^\circ) \rangle$.
The work is the dot product of these two vectors:
$$ W = \mathbf{F} \cdot \mathbf{D} = (70\cos(35^\circ))(100) + (70\sin(35^\circ))(0) = 7000\cos(35^\circ) \approx 5734 \text{ J} $$
Notice that this is just $W = |\mathbf{F}| |\mathbf{D}| \cos(\theta)$, which is the geometric definition of the dot product.
Check Your Understanding:
Problem: A constant force given by the vector $\mathbf{F} = \langle 5, 2, 1 \rangle$ (in Newtons) moves an object from the origin to the point $P(2, 4, 0)$ (in meters). Calculate the work done.
Conclusion
So today we've explored our first method of vector multiplication, the dot product. We've seen that it's much more than a simple calculation; it's a powerful tool for finding angles, checking for orthogonality, and calculating projections and physical quantities like work. The key takeaway is that the dot product tells you how much two vectors are aligned. Next time, we will explore the cross product, which will answer a very different question: how to find a vector that is perpendicular to two other vectors. 🚀